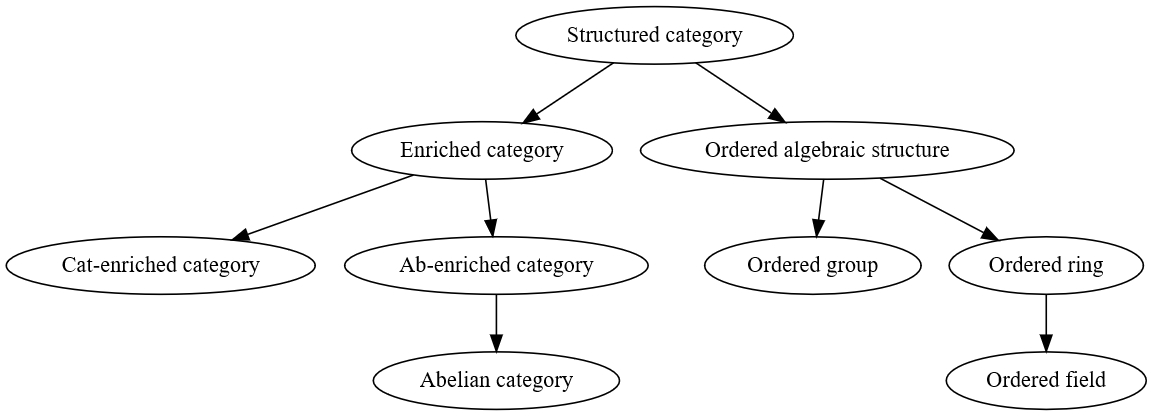
Posets are best classified as special types of thin categories, so it follows that ordered algebraic structures can be included in our ontology of categories with additional structure as described below.
Category element accessors:
There are a number of elements that define our access to the elements of a category: $Ob(C)$ for accessing all objects, $Arrows(C)$ for accessing all morphisms, and $Hom(A,B)$ for accessing all morphims from $A$ to $B$. These are the sets that we can establish additional structure on.
Overloading multimethods
So in order to implement categories with additional structure we can just describe ob, arrows, hom, etc as multimethods and then overloading them accordingly so that the appropriate kind of object is returned when accessing part of the category. So for an abelian category $Hom(X,Y)$ will return an abelian group, and for an ordered group $Ob(C)$ will return a group, and so on. This is how we can basically implement categories with additional structures in a computer algebra system.
No comments:
Post a Comment