Young's lattice is uniquely associated with a single conjugation automorphism:
\[ c : \mathbb{Y} \to \mathbb{Y} \]
Likewise each positive integer is associated to an additive partition in Young's lattice by its prime signature by the monotone $s$ mapping.
\[ s : \mathbb{Z}_+ \to \mathbb{Y} \]
This associates a young diagram to each positive integer, so that we can relate the symmetries of Young's lattice to the asymptotic distribution of the prime numbers of the positive integers. In particular, we have in Young's lattice that square free numbers {1,1,1,...} and prime powers {n} are conjugate.
Proposition. let $\mathbb{Y}$ be Young's lattice and let $\{1,1,1,...\}$ a sum of ones then its conjugate is a singleton $\{n\}$.
Proof. let $\{1,1,1,...\}$ be a sum of ones partition. Then the conjugate partition is the set $\{u_1,u_2,...\}$ with $u_1$ the number of terms less then or equal to one, $u_2$ the terms less then or equal to two, etc. But since all terms are less then one this always terminates to $\{n\}$ which is a singleton term. As the conjugation function is an involution, it follows that the conjugate of $\{n\}$ is a partition of the form $\{1,1,1,...\}$. $\square$
What this implies for the positive integers is that prime powers and square-free numbers should be basically symmetrical. But if we look at the Reimann zeta determined distribution of the prime numbers that is not what we get.
\[ \zeta(2) = \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6} \]
The probability that a positive integer is square free is equal to $\frac{1}{\zeta(2)}$ which is about $60$ percent. In fact a majority, or over half, of all positive integers are square free.
\[ \frac{1}{\zeta(2)} = \frac{6}{\pi^2} \approx 0.6 \]
Let us compare this to the probability that a given positive integer is a prime power. This is determined by the prime nmuber theorem.
\[ \lim_{x \to \infty} \frac{1}{ln(x)} \approx 0 \]
The situation isn't really any better when we extended this to arbitrary powers of $\ln(x)$ to get the probabilities of prime squares, prime cubes, etc. So in short, the probability any number is a prime power is zero.
\[ \lim_{x \to \infty} \sum_{n = 1}^{\infty} \frac{1}{ln(x)^n} \approx 0 \]
We can now compare the probabilities that a positive integer are square free or a prime power using the results determined by the Reimann zeta function and the prime number theorem.
\[ \text{square free} \approx 60\% \]
\[ \text{prime power} \approx 0\% \]
This is a startling result because you would expect by Young's lattice that square free numbers and prime powers should be symmetric, but the positive integers break this symmetry. There is a clear diversity bias among the positive integers, so that positive integers prefer a variety of different prime number factors over having a few that are the same.
Wednesday, February 23, 2022
Tuesday, February 22, 2022
Arithmetical properties of multiset systems
Perhaps the most basic object of mathematical discourse is that of a set system. This picture is complicated somewhat when we consider topos theory, and we start to consider copresheaf topoi which are about as fundamental as set systems. But we always can find ourselves looking back at concepts of set systems and hypergraphs. As we introduce and develop more forms of mathematical structure we can see set systems from different lights. We will see today how a semiring structure can be established on set systems.
Let $F(S)$ be a free commutative monoid on a set $S$. Then $\mathbb{N}F(S)$ is the semigroup semiring of all multiset systems whose terms are in $S$. We can now define an injective function that maps set systems into this semiring. \[ f: \wp(\wp(S)) \to \mathbb{N}F(S) \] With this we can treat set systems like any other arithmetic structure such as $\mathbb{N}$. In fact it is similar to $\mathbb{N}$ in a remarkable way: it is both additively and multiplicative J-trivial.
Proposition. let $\mathbb{N}F(S)$ be a semigroup semiring of multiset systems. Then both its additive and multiplicative parts are J-trivial commutative semigroups.
A semigroup semiring is additively J-trivial if its base semiring is. On the other hand, $\mathbb{N}F(S)$ is multiplicatively J-trivial because both the argument semigroup $F(S)$ and the multiplicative semigroup of the semiring are J-trivial. On the other hand, $\mathbb{Z}F(S)$ is clearly neither additively or multiplicatively J-trivial. We can always recover a J-trivial semigroup from a commutative semiring by quotienting out by the H classes.
Multiplication of set systems:
The definition of the multiplication of set systems follows easily from the definition of semigroup semirings. Algorithms can easily be provided for dealing with the multiplication of set systems by using for example either Clojure's list comprehensions or Java's for loops.
Definition. let $S$ and $T$ be indexed families of multiset systems. Let addition constitute the composition of multisets in a free commutative monoid. Then $ST$ can be defined by the sum: \[ \sum_{i \in I, j \in J} \{(S_i + T_j)\} \] This can be used to define our first examples of set system multiplication. Recall from the most basic of mathematics that an ordered pair is a set system of the form $\{\{a\},\{a, b \}\}$. I will first demonstrate the properties of set system multiplication by getting the powers of an ordered pair. \[ \{\{a\},\{a,b\}\}^2 = \{\{a,a\},\{a,a,b\},\{a,a,b\},\{a,a,b,b\}\} \] This process can naturally be continued to get yet higher powers of the ordered pair. The resulting multiset systems get quite large as the multiplication process continues. \begin{equation} \{\{a\},\{a,b\}\}^3 = \{\{a,a,a\},\{a,a,a,b\},\{a,a,a,b\},\{a,a,a,b,b\}, \\ \{a,a,a,b\},\{a,a,a,b,b\},\{a,a,a,b,b\},\{a,a,a,b,b,b\}\} \end{equation} In fact, the exact asymptotics of the growth of the cardinality of products of multiset systems is determined by a homomorphism of semigroups from the multiplication of set systems to the free commutative monoid.
Proposition. let $\mathbb{N}F(S)$ be the semigroup semiring of multiset systems. Let $|X|$ denote the cardinality of a multiset $X$. Then if $A$,$B$ are multiset systems we have that $|AB| = |A||B|$.
It follows that there is a homomorphism $f: (\mathbb{N}F(S),*) \to (\mathbb{N},*)$. Furthermore, it is not hard to see that this can be extended to a homomorphism of semirings $f: \mathbb{N}F(S) \to \mathbb{N}$.
Multiplicative factorisation of set systems:
We can now use the semigroup semiring $\mathbb{N}F(S)$ to interpret the properties of set systems.
Theorem. let $G$ be a complete bipartite graph between the sets $S$ and $T$. Then the binary family of edges of $G$ is the product of disjoint unary families formed from $S$ and $T$.
Proof. the complete bipartite graph has one edge ${s,t}$ for each $s \in S$ and each $t \in T$. On the other hand, the unary family of $S$ has one singleton $\{s\}$ for each $s \in S$ and likewise for $T$ there is one $\{t\}$ in the unary family of $T$ for each $t \in T$. Now given any $s \in S$ and $t \in T$ we get $\{s\} + \{t\} = \{s,t\}$ which is a set because $S$ and $T$ are disjoint. So the product of the unary families of $S$ and $T$ is the family of $G$. $\square$
This general process produces a multiplicative factorisation from complete bipartite binary families. We can now demonstrate this as an example of
Example. $\{\{a,x\},\{a,y\},\{b,x\},\{b,y\}\} = \{\{a\},\{b\}\}*\{\{x\},\{y\}\} $
With this approach, we can form a whole new algebraic theory of multiset systems. All the different set systems that emerge from graphs, partial orders, designs, matroids, etc can now be considered in a new light.
Foundations of combinatorial commutative algebra:
We have seen that commutative algebraic, and in particular the commutative semigroup semiring $\mathbb{N}F(S)$, can be used to better understand set systems and multiset systems. The dual concept is to use set systems as a tool of commutative algebra, which leads to combinatorial commutative algebra.
We have seen that multiset systems are elements of $\mathbb{N}F(S)$. There is an obvious correspondence from $\mathbb{N}F(S)$ to $\mathbb{Z}F(S)$, which extends the homomorphism $f: \mathbb{N} \to \mathbb{Z}$. \[ i : \mathbb{N}F^(S) \to \mathbb{Z}F(S) \] Where $\mathbb{Z}F(S)$ is in fact a ring of polynomials, because polynomial rings are nothing more then semigroup rings over free commutative monoids. Let $R$ be a commutative ring with identity $1$ then $R$ has a characteristic $C$ which means that extends over $GF(C)$. There is an obvious morphism $f: \mathbb{Z} \to GF(C)$ so that any non-zero characteristic prime ring is a quotient of $\mathbb{Z}$.
This naturally means that any integral polynomial in the semigroup ring $\mathbb{Z}F(S)$ can be embedded into a commutative ring with identity. This then produces a series of maps $\mathbb{N}F^(S) \to \mathbb{Z}F^{S} \to R F^(S)$ so that multiset systems are embeddable into arbitrary polynomial rings.
The Stanley-Reisner ring is nothing more then an application of this general construction in the case where $F$ is a field and the multiset system in question is the subclass closed set system of an abstract simplicial complex. The Stanley-Reisner ring is the simple the quotient ring determined by the monomial ideals of the set of this set system, but this could just as well be applied to get a quotient ring of a ring from arbitrary multiset systems.
See also:
[1] https://en.wikipedia.org/wiki/Stanley%E2%80%93Reisner_ring
Let $F(S)$ be a free commutative monoid on a set $S$. Then $\mathbb{N}F(S)$ is the semigroup semiring of all multiset systems whose terms are in $S$. We can now define an injective function that maps set systems into this semiring. \[ f: \wp(\wp(S)) \to \mathbb{N}F(S) \] With this we can treat set systems like any other arithmetic structure such as $\mathbb{N}$. In fact it is similar to $\mathbb{N}$ in a remarkable way: it is both additively and multiplicative J-trivial.
Proposition. let $\mathbb{N}F(S)$ be a semigroup semiring of multiset systems. Then both its additive and multiplicative parts are J-trivial commutative semigroups.
A semigroup semiring is additively J-trivial if its base semiring is. On the other hand, $\mathbb{N}F(S)$ is multiplicatively J-trivial because both the argument semigroup $F(S)$ and the multiplicative semigroup of the semiring are J-trivial. On the other hand, $\mathbb{Z}F(S)$ is clearly neither additively or multiplicatively J-trivial. We can always recover a J-trivial semigroup from a commutative semiring by quotienting out by the H classes.
Multiplication of set systems:
The definition of the multiplication of set systems follows easily from the definition of semigroup semirings. Algorithms can easily be provided for dealing with the multiplication of set systems by using for example either Clojure's list comprehensions or Java's for loops.
Definition. let $S$ and $T$ be indexed families of multiset systems. Let addition constitute the composition of multisets in a free commutative monoid. Then $ST$ can be defined by the sum: \[ \sum_{i \in I, j \in J} \{(S_i + T_j)\} \] This can be used to define our first examples of set system multiplication. Recall from the most basic of mathematics that an ordered pair is a set system of the form $\{\{a\},\{a, b \}\}$. I will first demonstrate the properties of set system multiplication by getting the powers of an ordered pair. \[ \{\{a\},\{a,b\}\}^2 = \{\{a,a\},\{a,a,b\},\{a,a,b\},\{a,a,b,b\}\} \] This process can naturally be continued to get yet higher powers of the ordered pair. The resulting multiset systems get quite large as the multiplication process continues. \begin{equation} \{\{a\},\{a,b\}\}^3 = \{\{a,a,a\},\{a,a,a,b\},\{a,a,a,b\},\{a,a,a,b,b\}, \\ \{a,a,a,b\},\{a,a,a,b,b\},\{a,a,a,b,b\},\{a,a,a,b,b,b\}\} \end{equation} In fact, the exact asymptotics of the growth of the cardinality of products of multiset systems is determined by a homomorphism of semigroups from the multiplication of set systems to the free commutative monoid.
Proposition. let $\mathbb{N}F(S)$ be the semigroup semiring of multiset systems. Let $|X|$ denote the cardinality of a multiset $X$. Then if $A$,$B$ are multiset systems we have that $|AB| = |A||B|$.
It follows that there is a homomorphism $f: (\mathbb{N}F(S),*) \to (\mathbb{N},*)$. Furthermore, it is not hard to see that this can be extended to a homomorphism of semirings $f: \mathbb{N}F(S) \to \mathbb{N}$.
Multiplicative factorisation of set systems:
We can now use the semigroup semiring $\mathbb{N}F(S)$ to interpret the properties of set systems.
Theorem. let $G$ be a complete bipartite graph between the sets $S$ and $T$. Then the binary family of edges of $G$ is the product of disjoint unary families formed from $S$ and $T$.
Proof. the complete bipartite graph has one edge ${s,t}$ for each $s \in S$ and each $t \in T$. On the other hand, the unary family of $S$ has one singleton $\{s\}$ for each $s \in S$ and likewise for $T$ there is one $\{t\}$ in the unary family of $T$ for each $t \in T$. Now given any $s \in S$ and $t \in T$ we get $\{s\} + \{t\} = \{s,t\}$ which is a set because $S$ and $T$ are disjoint. So the product of the unary families of $S$ and $T$ is the family of $G$. $\square$
This general process produces a multiplicative factorisation from complete bipartite binary families. We can now demonstrate this as an example of
Example. $\{\{a,x\},\{a,y\},\{b,x\},\{b,y\}\} = \{\{a\},\{b\}\}*\{\{x\},\{y\}\} $
With this approach, we can form a whole new algebraic theory of multiset systems. All the different set systems that emerge from graphs, partial orders, designs, matroids, etc can now be considered in a new light.
Foundations of combinatorial commutative algebra:
We have seen that commutative algebraic, and in particular the commutative semigroup semiring $\mathbb{N}F(S)$, can be used to better understand set systems and multiset systems. The dual concept is to use set systems as a tool of commutative algebra, which leads to combinatorial commutative algebra.
We have seen that multiset systems are elements of $\mathbb{N}F(S)$. There is an obvious correspondence from $\mathbb{N}F(S)$ to $\mathbb{Z}F(S)$, which extends the homomorphism $f: \mathbb{N} \to \mathbb{Z}$. \[ i : \mathbb{N}F^(S) \to \mathbb{Z}F(S) \] Where $\mathbb{Z}F(S)$ is in fact a ring of polynomials, because polynomial rings are nothing more then semigroup rings over free commutative monoids. Let $R$ be a commutative ring with identity $1$ then $R$ has a characteristic $C$ which means that extends over $GF(C)$. There is an obvious morphism $f: \mathbb{Z} \to GF(C)$ so that any non-zero characteristic prime ring is a quotient of $\mathbb{Z}$.
This naturally means that any integral polynomial in the semigroup ring $\mathbb{Z}F(S)$ can be embedded into a commutative ring with identity. This then produces a series of maps $\mathbb{N}F^(S) \to \mathbb{Z}F^{S} \to R F^(S)$ so that multiset systems are embeddable into arbitrary polynomial rings.
The Stanley-Reisner ring is nothing more then an application of this general construction in the case where $F$ is a field and the multiset system in question is the subclass closed set system of an abstract simplicial complex. The Stanley-Reisner ring is the simple the quotient ring determined by the monomial ideals of the set of this set system, but this could just as well be applied to get a quotient ring of a ring from arbitrary multiset systems.
See also:
[1] https://en.wikipedia.org/wiki/Stanley%E2%80%93Reisner_ring
Sunday, February 20, 2022
Semigroup semirings of multirelations
There are two main types of semigroup semiring used in relation theory: $\mathbb{N}F^{\to}(S)$ and $T_2F^{\to}(S)$. The former is the semiring of multirelations on a set constructed by the semiring $\mathbb{N}$, and the later is the semiring of relations constructed by the lattice semiring $T_2$.
The product of binary relations in a semigroup semiring is typically a quaternary multirelation, because the members of the resulting quaternary multirelation are defined by piecewise concatenation in their respective constituents. Semigroup semirings of multirelations are sort of like free rings in their construction by the free monoid. An interesting property of these semirings is that they are additively J-trivial and non-commutative.
Proposition. let $S$ be a non-trivial set then the semigroup semiring of multirelations $\mathbb{N}F^{\to}(S)$ is an additively J-trivial non-commutative semiring
Additively J-trivial semirings are interesting because they are inherently partially ordered algebraic structures. Indeed, their is a monomorphism of categories from additively j-trivial semirings to partially ordered semirings. Every semiring homomorphism is inherently monotone over J-preorders, so additively J-tivial semiring morphisms are morphisms of ordered semirings.
Idempotent semirings on the other hand abound. For example, the semiring of morphism systems of a semigroupoid is an infinite source of idempotent non-commutative semirings. So in that sense, $T_2F^{\to(S)}$ is just another non-commutative idempotent semiring and probably not as interesting as the semiring of multirelations.
Proposition. let $S$ be a set then the semigroup semiring of relations $T_2F^{\to}(S)$ is an idempotent non-commutative semiring.
One final semiring constuction related to relations is worth mentioning, which is the semiring of relations on a set which is isomorphic to the semiring of morphism systems of the complete thin groupoid. A notable difference between this and the semigroup semiring constructions is that it has restricted arity because it is not defined over a free monoid. The symmetric inverse semigroup, symmetric group, etc all embed in the multiplicative semigroup of relations.
- The semiring of multirelations: $\mathbb{N}F^{\to}(S)$
- The semiring of relations: $T_2 F^{\to}(S)$
The product of binary relations in a semigroup semiring is typically a quaternary multirelation, because the members of the resulting quaternary multirelation are defined by piecewise concatenation in their respective constituents. Semigroup semirings of multirelations are sort of like free rings in their construction by the free monoid. An interesting property of these semirings is that they are additively J-trivial and non-commutative.
Proposition. let $S$ be a non-trivial set then the semigroup semiring of multirelations $\mathbb{N}F^{\to}(S)$ is an additively J-trivial non-commutative semiring
Additively J-trivial semirings are interesting because they are inherently partially ordered algebraic structures. Indeed, their is a monomorphism of categories from additively j-trivial semirings to partially ordered semirings. Every semiring homomorphism is inherently monotone over J-preorders, so additively J-tivial semiring morphisms are morphisms of ordered semirings.
Idempotent semirings on the other hand abound. For example, the semiring of morphism systems of a semigroupoid is an infinite source of idempotent non-commutative semirings. So in that sense, $T_2F^{\to(S)}$ is just another non-commutative idempotent semiring and probably not as interesting as the semiring of multirelations.
Proposition. let $S$ be a set then the semigroup semiring of relations $T_2F^{\to}(S)$ is an idempotent non-commutative semiring.
One final semiring constuction related to relations is worth mentioning, which is the semiring of relations on a set which is isomorphic to the semiring of morphism systems of the complete thin groupoid. A notable difference between this and the semigroup semiring constructions is that it has restricted arity because it is not defined over a free monoid. The symmetric inverse semigroup, symmetric group, etc all embed in the multiplicative semigroup of relations.
Saturday, February 12, 2022
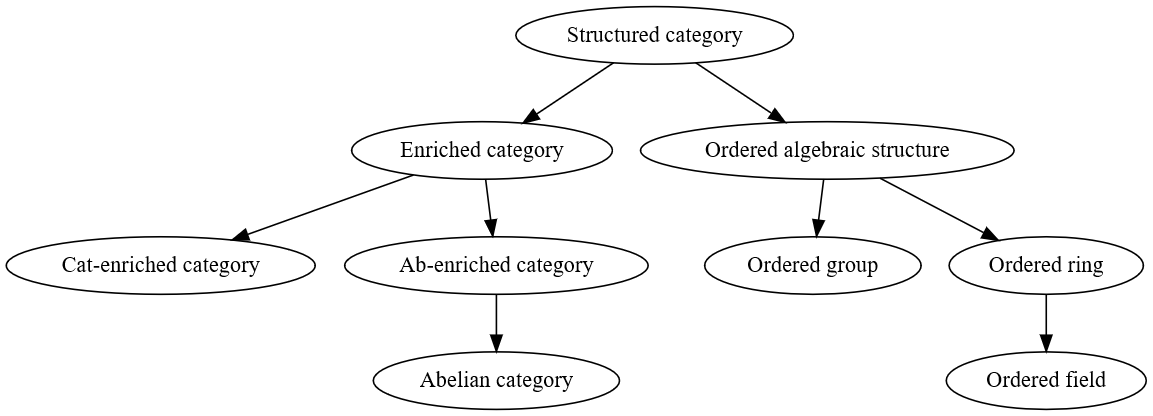
Structured categories
Posets are best classified as special types of thin categories, so it follows that ordered algebraic structures can be included in our ontology of categories with additional structure as described below.
Category element accessors:
There are a number of elements that define our access to the elements of a category: $Ob(C)$ for accessing all objects, $Arrows(C)$ for accessing all morphisms, and $Hom(A,B)$ for accessing all morphims from $A$ to $B$. These are the sets that we can establish additional structure on.
Overloading multimethods
So in order to implement categories with additional structure we can just describe ob, arrows, hom, etc as multimethods and then overloading them accordingly so that the appropriate kind of object is returned when accessing part of the category. So for an abelian category $Hom(X,Y)$ will return an abelian group, and for an ordered group $Ob(C)$ will return a group, and so on. This is how we can basically implement categories with additional structures in a computer algebra system.
There are a number of elements that define our access to the elements of a category: $Ob(C)$ for accessing all objects, $Arrows(C)$ for accessing all morphisms, and $Hom(A,B)$ for accessing all morphims from $A$ to $B$. These are the sets that we can establish additional structure on.
Overloading multimethods
So in order to implement categories with additional structure we can just describe ob, arrows, hom, etc as multimethods and then overloading them accordingly so that the appropriate kind of object is returned when accessing part of the category. So for an abelian category $Hom(X,Y)$ will return an abelian group, and for an ordered group $Ob(C)$ will return a group, and so on. This is how we can basically implement categories with additional structures in a computer algebra system.
Thursday, February 10, 2022
Preservation and reflection of subsemigroups
The functoriality of the Alexandrov topology of a thin category is a good first example of the broad theme of functorially produced set systems of algebraic structures. In order to continue along these lines we need to generalize from the category $Top$ of topological spaces and continuous maps to the categories of hypergraphs and either reflecting or preserving maps respectively. These produce functors that can be defined, for example over the category of semigroups.
Theorem. let $f : S \to T$ be a morphism of semigroups. Then $f$ preserves subsemigroups.
Proof. let $A \subseteq S$ then $\forall a_1,a_2 \in A: a1_a2 \in A$. So consider the image $f(A)$ and let $t_1,t_2 \in f(A)$ then there exists $a, b$ such that $f(a) = t_1$ and $f(b) = t_2$. Now consider the product $f(a)f(b)$ then by the definition of semigroup homomorphisms this is equal to $f(ab)$ but we have that $ab \in A$ so $t_1t_2 = f(ab) \in f(A)$ so that $f(A)$ is composition closed. $\square$
Theorem. let $f: S \to T$ be a morphism of semigroups. Then $f$ reflects subsemigroups.
Proof. let $B \subseteq T$ then $f^{-1}(B)$ is a subset of $S$. Suppose that $x,y \in f^{-1}(B)$ then $f(x) \in B$ and $f(y) \in B$. The product $f(xy)$ is equal to $f(x)f(y)$ by the definition of semigroup homomorphisms. Then since $f(x)$ is in $B$, $f(y)$ is in $B$ and $B$ is composition closed $f(xy) = f(x)f(y)$ is in $B$ which implies that $f^{-1}(B)$ is composition closed. $\square$
Theorem. let $f: M \to N$ be a morphism of monoids. Then $f$ preserves and reflect submonoids.
Proof. (1) let $S \subseteq M$ be a submonoid of $M$ then $1 \in S$ and by the definition of monoid homomorphisms $f(1)$ is the identity of $M$ so $1 \in f(S)$. (2) In the other direction, suppose that $S \subseteq M$ is a submonoid so that $1_N \in S$ then by the definition of monoid homomorphisms $f(1_M) = 1_M$ so that $1_M \in f^{-1}(S)$ so that monoid maps reflect identities. (3) then since $f$ preserves and reflects identities as well as subsemigroups it necessarily must also do so for submonoids as well. $\square$
Theorem. let $f: G \to H$ be a group homomorphism. Then $g$ preserves and reflects subgroups.
Proof. (1) let $S \subseteq G$ be a subgroup. Then for all $s \in S$ we have that $-s \in S$. Then consider $f(S)$ if $h$ is in $f(S)$ then we have that there exists $g$ such that $f(g) = h$. Then consider $-h$ by the definition of group homomorphisms $f(-g) = -h$ but then $-g$ is in $S$ because $S$ is a subgroup and therefore inverse closed. It follows that $f(-g) = -h$ is in $f(S)$ so that the image is a subgroup.
(2) in the other direction suppose that $S \subseteq H$ is a subgroup. Then $\forall s \in S : -s \in S$. Suppose that $g \in G$ and $f(g) \in S$. Then $f(-g) = -f(g)$ by the definition of group homomorphisms. By the fact that $S$ is a subgroup and $f(g)$ is in $S$ we have that $-f(g)$ is in $S$ which implies that $f^{-1}(S)$ is inverse closed for all $g \in f^{-1}(S)$. It follows that it is a subgroup. $\square$
We saw that monotone maps reflect ideals over thin categories. A generalization of this which is applicable to semigroups involves the reflection of semigroup ideals, which can be either left, right, or two sided. This produces a functor from the category of semigroups to the category of topological spaces.
Theorem. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects left, right, or two sided ideals.
Proof. let $I$ be a left ideal of $T$ then we have that for all $i \in I$ and $t \in T$ it holds that $it \in T$. So consider $f^{-1}(I)$ then if we have $x \in f^{-1}(I)$ it follows that $f(x) \in I$. Let $s \ in S$ then $f(sx) = f(s)f(x)$ and since $f(x)$ is in $I$ and $I$ is a left ideal $f(s)f(x)$ is in $I$. So $f$ reflects left ideals and by dualizing it reflects right ideals. By combining this $f$ reflects two sided ideals. $\square$
It is not enough for us to show that semigroup homomorphisms reflect subsemigroups. We would also like to know that they reflect prime ideals. This will then allow us to reproduce the familiar theorems of ring theory dealing with prime ideals.
Theorem. let $f : A \to B$ be a morphism of semigroups then $f$ reflects prime subsemigroups.
Proof. let $P \subseteq B$ be a prime subsemigroup then we have that $Q = B-P$ is a subsemigroup and in total we have $P,Q$ are subsemigroups with $P \cup Q = B$ and $P \cap Q = \emptyset$. Every element of $A$ produces some image, so by the fact that inverse images are lattice homomorphisms we have $f^{-1}(P) \cup f^{-1}(Q) = A$ and $f^{-1}(P) \cap f^{-1}(Q) = \emptyset$. So by the fact that $f$ reflects subsemigroups it follows that $f^{-1}(P)$ is a subsemigroup with complement subsemigroup $f^{-1}(Q)$. $\square$
Corollary. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects prime ideals.
The one other class of ideals we are really interested in are the radical ideals, especially in commutative algebra because of theri relationship to algebraic varieties under Hilbert'z nullstellensatz. There is a corresponding notion for semigroups, and so by considering that we will get closer to solving some problems related to radical subsemigroups and ideals.
Theorem. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects radical subsemigroups.
Proof. let $B \subseteq T$ be a radical subsemigroup. Then $f^{-1}(B)$ is a subsemigroup of $S$ because $f$ reflects subsemigroups, so it remains to show that $f^{-1}(B)$ is a radical subsemigroup. Let $x \in f^{-1}(B)$ and suppose that $y^n = x$ Then we can apply $f$ to both sides to get $f(y^n) = f(x)$ and expanding this $f(y)^n = f(x)$. Now since, $f(x)$ is in $B$ and $B$ is radical this implies that $f(y) \in B$. So to sum up this means that $f^{-1}(B)$ is a radical subsemigroup. $\square$
Corollary. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects semigroup radical ideals.
We can apply these semigroup theorems to our favourite algebraic structures, all of which are constructed out of semigroups. Like lattices (thin categories with all products and coproducts), semirings, and rings. In particular, this is enough to recover that the pre image of a prime ideal of a ring is a prime ideal.
Corollaries.
Theorem. let $f : S \to T$ be a morphism of semigroups. Then $f$ preserves subsemigroups.
Proof. let $A \subseteq S$ then $\forall a_1,a_2 \in A: a1_a2 \in A$. So consider the image $f(A)$ and let $t_1,t_2 \in f(A)$ then there exists $a, b$ such that $f(a) = t_1$ and $f(b) = t_2$. Now consider the product $f(a)f(b)$ then by the definition of semigroup homomorphisms this is equal to $f(ab)$ but we have that $ab \in A$ so $t_1t_2 = f(ab) \in f(A)$ so that $f(A)$ is composition closed. $\square$
Theorem. let $f: S \to T$ be a morphism of semigroups. Then $f$ reflects subsemigroups.
Proof. let $B \subseteq T$ then $f^{-1}(B)$ is a subset of $S$. Suppose that $x,y \in f^{-1}(B)$ then $f(x) \in B$ and $f(y) \in B$. The product $f(xy)$ is equal to $f(x)f(y)$ by the definition of semigroup homomorphisms. Then since $f(x)$ is in $B$, $f(y)$ is in $B$ and $B$ is composition closed $f(xy) = f(x)f(y)$ is in $B$ which implies that $f^{-1}(B)$ is composition closed. $\square$
Theorem. let $f: M \to N$ be a morphism of monoids. Then $f$ preserves and reflect submonoids.
Proof. (1) let $S \subseteq M$ be a submonoid of $M$ then $1 \in S$ and by the definition of monoid homomorphisms $f(1)$ is the identity of $M$ so $1 \in f(S)$. (2) In the other direction, suppose that $S \subseteq M$ is a submonoid so that $1_N \in S$ then by the definition of monoid homomorphisms $f(1_M) = 1_M$ so that $1_M \in f^{-1}(S)$ so that monoid maps reflect identities. (3) then since $f$ preserves and reflects identities as well as subsemigroups it necessarily must also do so for submonoids as well. $\square$
Theorem. let $f: G \to H$ be a group homomorphism. Then $g$ preserves and reflects subgroups.
Proof. (1) let $S \subseteq G$ be a subgroup. Then for all $s \in S$ we have that $-s \in S$. Then consider $f(S)$ if $h$ is in $f(S)$ then we have that there exists $g$ such that $f(g) = h$. Then consider $-h$ by the definition of group homomorphisms $f(-g) = -h$ but then $-g$ is in $S$ because $S$ is a subgroup and therefore inverse closed. It follows that $f(-g) = -h$ is in $f(S)$ so that the image is a subgroup.
(2) in the other direction suppose that $S \subseteq H$ is a subgroup. Then $\forall s \in S : -s \in S$. Suppose that $g \in G$ and $f(g) \in S$. Then $f(-g) = -f(g)$ by the definition of group homomorphisms. By the fact that $S$ is a subgroup and $f(g)$ is in $S$ we have that $-f(g)$ is in $S$ which implies that $f^{-1}(S)$ is inverse closed for all $g \in f^{-1}(S)$. It follows that it is a subgroup. $\square$
We saw that monotone maps reflect ideals over thin categories. A generalization of this which is applicable to semigroups involves the reflection of semigroup ideals, which can be either left, right, or two sided. This produces a functor from the category of semigroups to the category of topological spaces.
Theorem. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects left, right, or two sided ideals.
Proof. let $I$ be a left ideal of $T$ then we have that for all $i \in I$ and $t \in T$ it holds that $it \in T$. So consider $f^{-1}(I)$ then if we have $x \in f^{-1}(I)$ it follows that $f(x) \in I$. Let $s \ in S$ then $f(sx) = f(s)f(x)$ and since $f(x)$ is in $I$ and $I$ is a left ideal $f(s)f(x)$ is in $I$. So $f$ reflects left ideals and by dualizing it reflects right ideals. By combining this $f$ reflects two sided ideals. $\square$
It is not enough for us to show that semigroup homomorphisms reflect subsemigroups. We would also like to know that they reflect prime ideals. This will then allow us to reproduce the familiar theorems of ring theory dealing with prime ideals.
Theorem. let $f : A \to B$ be a morphism of semigroups then $f$ reflects prime subsemigroups.
Proof. let $P \subseteq B$ be a prime subsemigroup then we have that $Q = B-P$ is a subsemigroup and in total we have $P,Q$ are subsemigroups with $P \cup Q = B$ and $P \cap Q = \emptyset$. Every element of $A$ produces some image, so by the fact that inverse images are lattice homomorphisms we have $f^{-1}(P) \cup f^{-1}(Q) = A$ and $f^{-1}(P) \cap f^{-1}(Q) = \emptyset$. So by the fact that $f$ reflects subsemigroups it follows that $f^{-1}(P)$ is a subsemigroup with complement subsemigroup $f^{-1}(Q)$. $\square$
Corollary. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects prime ideals.
The one other class of ideals we are really interested in are the radical ideals, especially in commutative algebra because of theri relationship to algebraic varieties under Hilbert'z nullstellensatz. There is a corresponding notion for semigroups, and so by considering that we will get closer to solving some problems related to radical subsemigroups and ideals.
Theorem. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects radical subsemigroups.
Proof. let $B \subseteq T$ be a radical subsemigroup. Then $f^{-1}(B)$ is a subsemigroup of $S$ because $f$ reflects subsemigroups, so it remains to show that $f^{-1}(B)$ is a radical subsemigroup. Let $x \in f^{-1}(B)$ and suppose that $y^n = x$ Then we can apply $f$ to both sides to get $f(y^n) = f(x)$ and expanding this $f(y)^n = f(x)$. Now since, $f(x)$ is in $B$ and $B$ is radical this implies that $f(y) \in B$. So to sum up this means that $f^{-1}(B)$ is a radical subsemigroup. $\square$
Corollary. let $f : S \to T$ be a morphism of semigroups. Then $f$ reflects semigroup radical ideals.
We can apply these semigroup theorems to our favourite algebraic structures, all of which are constructed out of semigroups. Like lattices (thin categories with all products and coproducts), semirings, and rings. In particular, this is enough to recover that the pre image of a prime ideal of a ring is a prime ideal.
Corollaries.
- Lattice homomorphisms preserve and reflect sublattices
- Semigroup homomorphisms preserve and reflect subsemirings
- Ring homomorphisms preserve and reflect subrings
- Ring homomorphisms reflect left, right, and two sided ideals, prime ideals, and radical ideals
Wednesday, February 9, 2022
Functorality of the Alexandrov topology
A number of set systems associated to structured sets either preserve or reflect substructures and they therefore form functors to categories of hypergraphs or topologies. The Alexandrov topology consisting of all lower sets (respectively upper sets) of a poset is a basic example.
Lemma 1. Let $f: A \to B$ be a monotone map of posets. Let $L$ be a lower set of $B$, then $f^{-1}(L)$ is a lower set of $A$.
Proof. suppose that $a \in f^{-1}(L)$ then $f(a) \in L$ and further suppose that $b \subseteq a$. By the fact that $f$ is monotone we have $f(a) \subseteq f(b)$ and now by the fact that $f(b) \in L$ and $L$ is a lower set, we have that $f(a) \in L$. Which implies that $a \in f^{-1}$ so in short $b \subseteq a \text{ and } a \in f^{-1}(L)$. Therefore, $f^{-1}(L)$ is a lower set.
The dual proposition that monotone maps preserve lower sets is trivially false, consider $F : 1 \to 3$ that maps the singleton poset to the middle element of an ordered triple. Then this map preserves neither upper sets or lower sets. So the Alexandrov topology is not functorial to the category of topologies and open maps, but it is for the more relevent category $Top$ of topologies and continuous maps.
Theorem 1. $F: Ord \to Top$ is a covariant functor from the category of thin categories to the category of topological spaces and continuous maps.
Proof. (1) let $P$ be a thin category then $F(P)$ is the topology generated by the map of singletons that produces all predecessor elements and this is trivially an Alexandrov topology (2) and by lemma 1 for any functor $f : A \to B$ we have that $F(f) : F(A) \to F(B)$ is a continuous map. Finally (3) $F$ preserves composition by preserving underlying functions so $F$ is functorial. $\square$
The fact that monotone maps reflect lower sets (respectively upper sets) is simply a long line of a group of theorems dealing with the preservation and reflection of open sets. For example, the fact that the pre image of a prime ideal is a prime ideal is used in commutative algebra to describe the functoriality of the topology $Spec(R)$. We see that order ideals are not that different from ring ideals.
Lemma 1. Let $f: A \to B$ be a monotone map of posets. Let $L$ be a lower set of $B$, then $f^{-1}(L)$ is a lower set of $A$.
Proof. suppose that $a \in f^{-1}(L)$ then $f(a) \in L$ and further suppose that $b \subseteq a$. By the fact that $f$ is monotone we have $f(a) \subseteq f(b)$ and now by the fact that $f(b) \in L$ and $L$ is a lower set, we have that $f(a) \in L$. Which implies that $a \in f^{-1}$ so in short $b \subseteq a \text{ and } a \in f^{-1}(L)$. Therefore, $f^{-1}(L)$ is a lower set.
The dual proposition that monotone maps preserve lower sets is trivially false, consider $F : 1 \to 3$ that maps the singleton poset to the middle element of an ordered triple. Then this map preserves neither upper sets or lower sets. So the Alexandrov topology is not functorial to the category of topologies and open maps, but it is for the more relevent category $Top$ of topologies and continuous maps.
Theorem 1. $F: Ord \to Top$ is a covariant functor from the category of thin categories to the category of topological spaces and continuous maps.
Proof. (1) let $P$ be a thin category then $F(P)$ is the topology generated by the map of singletons that produces all predecessor elements and this is trivially an Alexandrov topology (2) and by lemma 1 for any functor $f : A \to B$ we have that $F(f) : F(A) \to F(B)$ is a continuous map. Finally (3) $F$ preserves composition by preserving underlying functions so $F$ is functorial. $\square$
The fact that monotone maps reflect lower sets (respectively upper sets) is simply a long line of a group of theorems dealing with the preservation and reflection of open sets. For example, the fact that the pre image of a prime ideal is a prime ideal is used in commutative algebra to describe the functoriality of the topology $Spec(R)$. We see that order ideals are not that different from ring ideals.
Sunday, February 6, 2022
Composition homomorphisms and partial algebras
The basic universal algebraic framework for dealing with total algebras, consisting of a set of elements $S$ and a set of n-ary operator functions on it $f: S^n \to S$ needs to be extended to deal with partial algebras, such as the partial composition semigroup of a category. The key to this construction it turns out is simply the construction of a relation homomorphism of the domains of the two partial algebras.
Definition. let $A$ be a set and $R \subseteq A^n$ an n-ary relation on $A$. Then there exists an inclusion function $i_R : R \hookrightarrow A^n$ associated with $R$. A partial algebra on $R$ is then simply a function $f: R \to A$.
We can freely define any kind of function we want, but in order to get a valid category we also need to define morphisms. The first component to that will be the definition of composition relation homomorphisms.
Definition. let $(A,f: R \to A)$ and $(B,g : S \to B)$ be n-ary partial algebras. Then $m : A \to B$ is a composition relation homomorphism provided that $m : (A,R) \to (B,S)$ is a homomorphism of relations meanining that $(a_1,a_2,...) \in R$ implies that $(f(a_1),f(a_2),...) \in S$.
In the case of total algebras, we don't need a relation homomorphism. On the other hand, since partial algebras are defined over arbitrary n-ary relations we need the composition relation homomorphism to ensure the validity of the partial algebra homomorphism construction.
Definition. let $(A,f: R \to A)$ and $(B,g : S \to B)$ be n-ary partial algebras. Then $m : A \to B$ is a partial algebra homomorphism provided that (1) it is a composition relation homomorphism and (2) $f(a_1,a_2,...) = g(m(a_1),m(a_2),...)$ for any $(a_1,a_2,...) \in R$. The first condition ensures that $(m(a_1),m(a_2),...)$ actually exists and is in the domain of $g$. The second condition ensures that they are also equal.
A category is simply a special combination of objects and morphisms so now that we have the preliminary definitions out of the way we can define the category of partial nary algebras.
Definition. let $n \in \mathbb{N}$ then $PA_n$ is the category of $n-ary$ partial algebras with homomorphisms previously defined. The composition domain is a forgetful functor $D : PA_n \to Rel_n$ from this categroy to the category of nary relations.
In order to continue, we now need to prove a basic lemma about relation homomorphisms. This will allow us to construct the input function component of the morphism of functions in the topos $Sets^{\to}$ that emerges from partial algebra homomorphisms.
Lemma 1. let $f : (A,R) \to (B,S)$ be a homomorphism of n-ary relations then consider the product function $f^n : A^n \to B^n$ of the underlying function $f$. Then $(R,S)$ defines a subfunction of $f^n$ in the topos of functions.
Proof. in order for $(R,S)$ to be a subfunction of $f^n$ then it must be that for all $(a_1,a_2,...) \in R$ we have that $(f(a_1),f(a_2),...)$ but this is precisely the definition of a relation homomorphism. $\square$
Then we can restrict $f^n$ to $f^n_{R,S}$ to a get a monomorphism in the topos of functions as depicted in the commutative diagram below. The point of this construction is to enable us to prove our main theorem which is that homomorphisms of partial nary functional algebras as we have defined them induce morphisms in the topos of functions $Sets^{\to}$.
The point of this construction is to enable us to prove our main theorem which is that homomorphisms of partial nary functional algebras as we have defined them induce morphisms in the topos of functions $Sets^{\to}$.
Theorem 1. let $m : (A, \circ_A : R \to A) \to (B, \circ_B : S \to B)$ be a homomorphism of partial n-ary functional algebras. Then $(m^n_{(R,s) : R \to S},m: A \to B)$ is a morphism of functions from $\circ_A$ to $\circ_B$.
Proof. by lemma 1 we have that $f^n_{R,S}$ is a well defined function. By the definition of partial algebra homomorphisms we have that for each $(a_1,a_2,...) \in R$ that $f(\circ_A(a_1,a_2,..)) = \circ_B(f(a_1),f(a_2),...)$. It follows that $f \circ \circ_A = \circ_B \circ f^{n_{(R,S)}}$ as depited in the following commutative diagram. It follows that $(m^n_{(R,s) : R \to S},m: A \to B)$ is a morphism in the topos of functions $Sets^{\to}$. It follows that $F : PA_n \to Sets^{\to}$ is a monomorphism from the category of partial algebras to the topos of functions. $\square$
It follows that $(m^n_{(R,s) : R \to S},m: A \to B)$ is a morphism in the topos of functions $Sets^{\to}$. It follows that $F : PA_n \to Sets^{\to}$ is a monomorphism from the category of partial algebras to the topos of functions. $\square$
This allows us to create a topos theoretic model for theory of partial algebras. We can now apply this to categories by definining the composition function of a category as a partial algebra.
Definition. let $(Ob(C),Arrows(C),source,target,id,\circ)$ be a category then $(Arrows(C), \circ : Arrows(C)^2_* \to Arrows(C))$ is a partial binary algebra defined over the morphism set of $C$.
Firstly, we can naturally relate functors to homomorphisms of composition relations. This produces a natural forgetful functor from the category of categories $Cat$ to the category of binary relations $Rel$ and relation homomorphisms.
Lemma 2. let $F: C \to D$ then $F$ induces a homomorphism of binary relations from $Arrows(C)^2_*$ to $Arrows(D)^2_*$.
Proof. let $m_1 : A \to B$ and $m_2 : C \to D$ be morphisms of $C$ then in order for them to be composable we humst have $B=C$. Then by the definition of functors, we have that $f(m_1) : f(A) \to f(B)$ and $f(m_2) : f(C) \to f(D)$ are the object signatures of $f(m_1)$ and $f(m_2)$. The fact that $B=C$ implies that $f(B) = f(C)$. It follows that $f(m_1)$ and $f(m_2)$ are composable, so that if $m_1$ and $m_2$ are composable then their outputs by $f$ are. It follows that the morphic component of $F$ is a homomorphism of composition relations. $\square$.
Lemma 3. let $F : C \to D$ be a functor then $F$ induces a homomorphism of partial algebras $PA_F : (Arrows(C)^2_*, \circ) \to (Arrows(D)^2_*, \circ)$.
Proof. in order for a function to be a partial algebra homomorphism it must satisfy two conditions. Condition (1) is satisfied by lemma 2. Condition (2) follows immediately from the definition of functors which ensures that $f(m_1 \circ m_2) = f(m_1) \circ f(m_2)$ whenever the two exist.
We started this discussion by relating the category $PA_n$ to the topos of functions $Sets^{\to}$. With this preliminary out of the way, we can now relate the category of categories $Cat$ itself to the topos of functions $Sets^{\to}$ by defining a forgetful functor from any category to its composition function.
Theorem 2. let $\circ : Cat \to Sets^{\to}$ be the function that maps any category to its underlying composition function, and any functor to its morphism of composition functions. Then $\circ$ is a forgetful functor from the category of categories to the topos of functions.
Proof. by lemma 3 we have a functor $Cat \to PA_2$ from $Cat$ to partial binary algebras. By theorem 1, we can then compose this with the functor from $PA_2$ to $Sets^{\to}$ to get a functor from $Cat$ to $Sets^{\to}$. $\square$
There are two main functors from $Cat$ to topoi the underlying quiver $q : Cat \to Quiv$ and the underlying composition functor $\circ : Cat \to Sets^{\to}$. The other topos valued functors from $Cat$ can be defined by composition with these functors, like the functor to $Sets^2$ or the different functors to $Sets$ defined by taking the object set or the morphism set of the category.
Definition. let $A$ be a set and $R \subseteq A^n$ an n-ary relation on $A$. Then there exists an inclusion function $i_R : R \hookrightarrow A^n$ associated with $R$. A partial algebra on $R$ is then simply a function $f: R \to A$.
We can freely define any kind of function we want, but in order to get a valid category we also need to define morphisms. The first component to that will be the definition of composition relation homomorphisms.
Definition. let $(A,f: R \to A)$ and $(B,g : S \to B)$ be n-ary partial algebras. Then $m : A \to B$ is a composition relation homomorphism provided that $m : (A,R) \to (B,S)$ is a homomorphism of relations meanining that $(a_1,a_2,...) \in R$ implies that $(f(a_1),f(a_2),...) \in S$.
In the case of total algebras, we don't need a relation homomorphism. On the other hand, since partial algebras are defined over arbitrary n-ary relations we need the composition relation homomorphism to ensure the validity of the partial algebra homomorphism construction.
Definition. let $(A,f: R \to A)$ and $(B,g : S \to B)$ be n-ary partial algebras. Then $m : A \to B$ is a partial algebra homomorphism provided that (1) it is a composition relation homomorphism and (2) $f(a_1,a_2,...) = g(m(a_1),m(a_2),...)$ for any $(a_1,a_2,...) \in R$. The first condition ensures that $(m(a_1),m(a_2),...)$ actually exists and is in the domain of $g$. The second condition ensures that they are also equal.
A category is simply a special combination of objects and morphisms so now that we have the preliminary definitions out of the way we can define the category of partial nary algebras.
Definition. let $n \in \mathbb{N}$ then $PA_n$ is the category of $n-ary$ partial algebras with homomorphisms previously defined. The composition domain is a forgetful functor $D : PA_n \to Rel_n$ from this categroy to the category of nary relations.
In order to continue, we now need to prove a basic lemma about relation homomorphisms. This will allow us to construct the input function component of the morphism of functions in the topos $Sets^{\to}$ that emerges from partial algebra homomorphisms.
Lemma 1. let $f : (A,R) \to (B,S)$ be a homomorphism of n-ary relations then consider the product function $f^n : A^n \to B^n$ of the underlying function $f$. Then $(R,S)$ defines a subfunction of $f^n$ in the topos of functions.
Proof. in order for $(R,S)$ to be a subfunction of $f^n$ then it must be that for all $(a_1,a_2,...) \in R$ we have that $(f(a_1),f(a_2),...)$ but this is precisely the definition of a relation homomorphism. $\square$
Then we can restrict $f^n$ to $f^n_{R,S}$ to a get a monomorphism in the topos of functions as depicted in the commutative diagram below.
 The point of this construction is to enable us to prove our main theorem which is that homomorphisms of partial nary functional algebras as we have defined them induce morphisms in the topos of functions $Sets^{\to}$.
The point of this construction is to enable us to prove our main theorem which is that homomorphisms of partial nary functional algebras as we have defined them induce morphisms in the topos of functions $Sets^{\to}$.
Theorem 1. let $m : (A, \circ_A : R \to A) \to (B, \circ_B : S \to B)$ be a homomorphism of partial n-ary functional algebras. Then $(m^n_{(R,s) : R \to S},m: A \to B)$ is a morphism of functions from $\circ_A$ to $\circ_B$.
Proof. by lemma 1 we have that $f^n_{R,S}$ is a well defined function. By the definition of partial algebra homomorphisms we have that for each $(a_1,a_2,...) \in R$ that $f(\circ_A(a_1,a_2,..)) = \circ_B(f(a_1),f(a_2),...)$. It follows that $f \circ \circ_A = \circ_B \circ f^{n_{(R,S)}}$ as depited in the following commutative diagram.
 It follows that $(m^n_{(R,s) : R \to S},m: A \to B)$ is a morphism in the topos of functions $Sets^{\to}$. It follows that $F : PA_n \to Sets^{\to}$ is a monomorphism from the category of partial algebras to the topos of functions. $\square$
It follows that $(m^n_{(R,s) : R \to S},m: A \to B)$ is a morphism in the topos of functions $Sets^{\to}$. It follows that $F : PA_n \to Sets^{\to}$ is a monomorphism from the category of partial algebras to the topos of functions. $\square$
This allows us to create a topos theoretic model for theory of partial algebras. We can now apply this to categories by definining the composition function of a category as a partial algebra.
Definition. let $(Ob(C),Arrows(C),source,target,id,\circ)$ be a category then $(Arrows(C), \circ : Arrows(C)^2_* \to Arrows(C))$ is a partial binary algebra defined over the morphism set of $C$.
Firstly, we can naturally relate functors to homomorphisms of composition relations. This produces a natural forgetful functor from the category of categories $Cat$ to the category of binary relations $Rel$ and relation homomorphisms.
Lemma 2. let $F: C \to D$ then $F$ induces a homomorphism of binary relations from $Arrows(C)^2_*$ to $Arrows(D)^2_*$.
Proof. let $m_1 : A \to B$ and $m_2 : C \to D$ be morphisms of $C$ then in order for them to be composable we humst have $B=C$. Then by the definition of functors, we have that $f(m_1) : f(A) \to f(B)$ and $f(m_2) : f(C) \to f(D)$ are the object signatures of $f(m_1)$ and $f(m_2)$. The fact that $B=C$ implies that $f(B) = f(C)$. It follows that $f(m_1)$ and $f(m_2)$ are composable, so that if $m_1$ and $m_2$ are composable then their outputs by $f$ are. It follows that the morphic component of $F$ is a homomorphism of composition relations. $\square$.
Lemma 3. let $F : C \to D$ be a functor then $F$ induces a homomorphism of partial algebras $PA_F : (Arrows(C)^2_*, \circ) \to (Arrows(D)^2_*, \circ)$.
Proof. in order for a function to be a partial algebra homomorphism it must satisfy two conditions. Condition (1) is satisfied by lemma 2. Condition (2) follows immediately from the definition of functors which ensures that $f(m_1 \circ m_2) = f(m_1) \circ f(m_2)$ whenever the two exist.
We started this discussion by relating the category $PA_n$ to the topos of functions $Sets^{\to}$. With this preliminary out of the way, we can now relate the category of categories $Cat$ itself to the topos of functions $Sets^{\to}$ by defining a forgetful functor from any category to its composition function.
Theorem 2. let $\circ : Cat \to Sets^{\to}$ be the function that maps any category to its underlying composition function, and any functor to its morphism of composition functions. Then $\circ$ is a forgetful functor from the category of categories to the topos of functions.
Proof. by lemma 3 we have a functor $Cat \to PA_2$ from $Cat$ to partial binary algebras. By theorem 1, we can then compose this with the functor from $PA_2$ to $Sets^{\to}$ to get a functor from $Cat$ to $Sets^{\to}$. $\square$
There are two main functors from $Cat$ to topoi the underlying quiver $q : Cat \to Quiv$ and the underlying composition functor $\circ : Cat \to Sets^{\to}$. The other topos valued functors from $Cat$ can be defined by composition with these functors, like the functor to $Sets^2$ or the different functors to $Sets$ defined by taking the object set or the morphism set of the category.
Subscribe to:
Comments (Atom)